Formalism

A nice way of thinking about maths.

I have a few big posts in the making, but I haven’t found a good way to publish them yet. Given that I haven’t posted in a while, I decided to practice with shorter posts for now.

Introduction

I believe formalism is a good way of thinking about maths. It is a common conversation topic of mine, and I have much to say about it.

The formalist approach is one of the greatest tools that humanity has come up with to systematically tackle problems. Formalism is now everywhere, and it is to a great extent what makes a field of science hard.

Nevertheless, I find it quite misunderstood, and believe we could still leverage it more.

To get a feel for the kind of answers formalism brings to the table, you may want to think seriously about the following questions: What is maths? Why does maths work? And when does maths not work?

Answering those questions is not trivial. It is not that we have no intuitions behind the answers. It is more that it is hard to pin them down, put words on them, or even… reason about them mathematically.

Mathematics, the science of… what?

History is the study of the past. Geography is the study of the world and maps. English is the study of written texts. But what does maths study?

It is about numbers, functions, lines, shapes, logic, algorithms, and then some more. While this makes for an impressive range of sub-fields, it is not obvious what the central topic is here.

Coming up with the common factor for all of this is not easy. As written on Wikipedia: There is no general consensus among mathematicians about a common definition for their academic discipline.

—

Maths might be about abstractions, as opposed to concrete things? But that’s not saying much. All fields of inquiry are about abstraction to some extent.

For instance, taking data from astronomy, astrophysics builds and studies abstract models of celestial bodies. Similarly, geography abstracts the study of ground-level territories into that of countries.

Abstraction is not specific to mathematics, which started with the very concrete activity of counting. Abstraction is just a normal part of thinking and generalising. If one were to think of the relation between mathematics and abstraction, a fruitful question might be “In the first place, what is mathematics even trying to abstract?”.

—

Then, maths might be about formal proofs? We start with axioms, then do some logic on them, applying rules and stuff, and at the end we get theorems? Nope. Still not it. Proving theorems is not the object of maths, theorems and proofs are merely tools, useful as compact summaries.

We have been doing maths long before we proved theorems. Both as humanity and as individuals, we have added and multiplied numbers before we developed the idea of rigorously proving theorems. And even then, we were able to use the Pythagorean theorem before we proved it.

—

Ok, let’s finally answer the question, what is maths actually about?

Meaningless Symbols

From the formalist point of view, maths is the study of what you can do with meaningless symbols. Sometimes, symbols are referred to as syntactic forms, which is where the name “formalism” comes from.

On a deep level, maths is like football. It is popular (although with different people) because it can be played anywhere. To play football, we need a ball, and that’s all. The ball doesn’t mean anything, it is just a thing you can play with. We don’t even need goals, we can always kick up, dribble, or pass the ball around.

Similarly, to play maths, we just need symbols.

—

I don’t think there is a standard definition for symbols, and I have mentioned them twice already. So here is mine: a symbol is a stable object, that we can easily compare to others, and move around.

By “stable”, I don’t mean anything deep. I just mean that it should not unexpectedly disappear, wear off, move, split, divide or duplicate itself. Something like “If I write letters on a sheet of paper, I don’t expect that they just get messed up whenever I stop looking at them, as in dreams.”.

And by “compare”, I mean something simple too. Like, you should be able to check whether two symbols are the same and whether they are different. Fundamentally, even if I write badly, as long as we can both agree that my 0 is a 0, that your 1 is a 1, and that 0 and 1 are different, then they count as symbols and we can use them to do maths together.

—

As long as those constraints are met, we can use anything as a symbol. Ink drawings on paper, electrons in computers, weird signs like ∯ and ⋢, our own fingers when we count on them, or lines in the sand (as long as there’s no wind).

It truly doesn’t matter. There’s no magic to it: meet the constraints, and you’ve gotten yourself symbols.

—

We can even use people as symbols.

Here is some people-based maths: put 8 people in the room, 7 in another, tell them to get together in the same room, count the number of people in that room, and boom, you have implemented addition by using people as symbols.

The constraint of “being a stable object” shines here: if the people started unexpectedly changing rooms, then the addition would fail, because the people involved would not have been good stable symbols.

—

Maths is fundamentally the study of symbol manipulation. You’ve got symbols, you start moving them around, you study what happens, and here you go: you are doing maths. That’s it. No more, no less.

A key point is that to play with symbols, you do not need to care about what they represent or what they mean. Indeed, in maths, the symbols are meaningless. They do not represent anything. When learning advanced maths, it is actually a common pitfall to try too much to think of mathematical symbols as signifiers that mean things, as opposed to computational devices that you move around according to rules.

Why does maths work?

Regardless of whether you subscribe to formalism or not, there is a big mystery around maths. Why, by just moving around symbols and following miscellaneous rules, do we get to predict various aspects of reality? Where’s the magic?

I looked for the standard explanation on Google and even asked ChatGPT, but I ended up cringing. The answers are long-winded, and/or use complicated words like “axioms”, “consistency”, “logic”, and “abstraction”, with these words making things less clear. My cynical take is that these answers hide a lack of understanding of the topic.

—

Maths works because the same symbol manipulations yield the same results. That’s it. I find anything more complicated than that tiring and sad.

Those symbol manipulations go by many different names, depending on the context: algorithms, computation, programs, calculations, equation solving, integration, rewriting systems, formal proofs, and many more. 

—

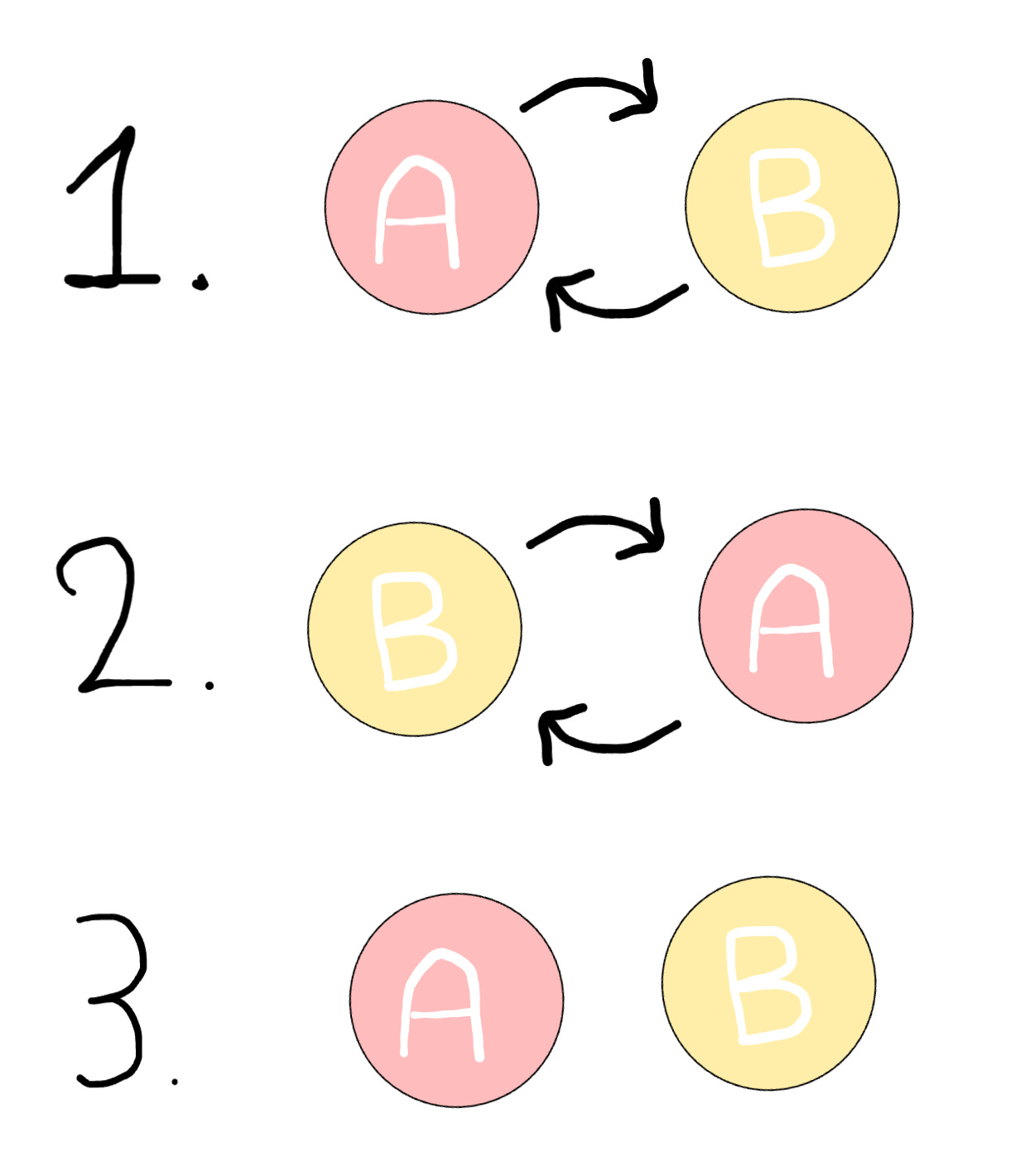
Let’s dig into the simple magic of symbol manipulation with an example. To do so, let’s study a very deep theorem of maths:

Gabe’s Double-Swap Theorem (GDS Theorem): If you put the symbols A and B in that order, and you swap them twice, they end up back in the same order.

Here is a graphical representation of the theorem:

A nice picture of the GDS Theorem

This is a genuine theorem of maths, in its own right. It might not be studied in classes, and its name might not be standard, but it does capture the essence of maths.

You can try to apply it yourself, right now, where you are, and see that it works. Take two items that will not spontaneously combust and that you can distinguish, like a full glass of water, and an empty glass of water. Swap them around. Then swap them again. They should then end up in the same order.

If you have people with you, you can also have them act as symbols, just make sure they don’t start randomly moving when they should not.

The GDS theorem features the two crucial components of maths. The symbols (A and B). And symbol manipulations, namely, arranging symbols in some order, and swapping them.

—

This example is straightforward enough that it should be clear why it works: in both the theorem, and the home-experiment setup, the same thing is happening.

Our universe is such that very often, the same causes lead to the same effects. With maths, we are leveraging this. We constrain symbols strongly enough that, by definition, when we perform the same manipulation on our symbols, it leads to the same results. Wherever those symbols might be, whoever (or whatever) might perform those manipulations, the results are the same.

To the extent that some process in the real world is similar to some symbol manipulation, we can perform that symbol manipulation on paper, ahead of time, to predict the outcome of that real-world process. And by doing so, we predict much more than the outcome of that specific process, we learn what happens in all the places in the world where there is something similar to that symbolic manipulation.

We can make it more specific by focusing on addition. It means that when you calculate an addition, through mental arithmetic, pen and paper or a calculator, you can predict the result of all the things in the real world that are similar to that addition. So, if you computed 7 + 8, then by doing this, you now have between your hands a universal prediction: you know what will happen whenever someone tries to count the number of items from any two groups of 7 and 8 items that merge.

This is why maths works, and how it is so powerful. It is the field that pushes the most basic, consistent and cheap-to-reproduce patterns, the symbolic manipulations, to their limit. Maths specialises in exploiting universal patterns that are easy to reproduce with a pen and paper.

Symbolic manipulations are so reliable that you can string together quadrillions of them in a row, and still get reproducible outputs. We just live in an incredibly consistent universe.

And it so happens that in our universe, we can go a long way by combining symbolic manipulations.

When does maths fail?

Maths is not magic. The mathematical process is not “I describe something with symbols, I play with them a bit, I get some result, and then reality happens to shape to match it”.

Sometimes, we try to model something mathematically (as in, with symbol manipulation), and we fail. How can we predict when it happens? By what logic can we know whether some process in reality will match or not some symbolic manipulation? 

To understand this, I think it helps to distinguish between two types of failures.

—

The first one is when we thought we understood what was happening in the real world, but we did not. This is the common pitfall of naive modelling: thinking that because we can create simple scientific models, that the world itself must be simple.

This is the core part of science, the interplay between theory and practice. We must investigate the world, to get enough information about what is happening, so that we can then mimic the movement of things through symbolic manipulations.

This is what it means to formally model something. And whenever the maths skips some important dynamic of the world with its symbolic representations, it fails.

—

The second failure is when we did understand what was happening in the real-world, but did not understand our own symbolic manipulation.

This is slightly more subtle than the first type. In the first type, we have a model of reality, but reality does not match it.

In this type of failure, we are wrong not about reality, but about our own model.

The simplest such failure is when you get a wrong answer because you messed up your calculation itself. Like, you understood the situation well, you had a good model, and then you made a basic error in your calculations.

An unfortunate bird who made an error of the second type.

Another famous example from programming is an actual bug that prevented a computer from functioning, coming from Grace Hopper. This is an example where we missed information not about the reality that we tried to model, but about our own model. In that case, we missed the fact that there was an actual bug in the computer, the part of our model that performed the calculation.

The log book featuring the infamous bug.

—

You can always go deeper with these types of failures. For instance, you could refine them into “not gathering enough real-world data”, “missing a crucial consideration”, “not keeping track of your assumptions”, “using the wrong mathematical tool”, “programming errors”, etc. The point is not that in maths, there are two objectively correct and standard types of failures.

The point is that formalism helps with reliably thinking about this problem. It is a view that is precise enough that it lets you categorise failures, and make sense of all of them, rather than just relying on intuition. Maths only works to the extent that its symbolic manipulations reflect what is actually happening in reality, and to the extent that those symbolic manipulations are performed correctly.

Conclusion

I think the formalist point of view helps in explaining various aspects of mathematics.

What is maths? Maths is the study of symbol manipulation.

Why does maths work? Maths works because it focuses on symbol manipulations: extremely reliable and universal processes. Whenever we notice a process similar to some symbol manipulation, we can perform it ourselves (with a pen and a paper, for instance), and predict the outcome of that process.

When does maths not work? Maths fails when we fail to mimic a naturally occurring process occurring with symbol manipulation, or when we fail at understanding or correctly performing our own symbolic manipulation.

Those are still superficial questions, but I believe formalism can also help with answering deeper questions. Consider:

• How can you use maths in real life? What is the minimum that you need to learn to build your own mathematical models?

• What is the connection between logic, maths and computer science?

• What is the relationship between mathematical progress and the introduction of novel mathematical symbols?

• Why are some abstract models so much more useful than others? How can we predict in advance which type of maths will be useful?

• How can different models lead to the same results? When are they equivalent?

People often confuse maths for advanced functional analysis and geometry, and expect maths to be much more magical and complex than it is. As a result, maths isn’t used and taught nearly widely enough.

For instance, I believe that smart non-researchers could start building their own mathematical models, relevant to their own field of expertise, after less than a hundred hours of training.

Similarly, I believe that through the use of mathematical modelling, moral philosophy could make paradoxes clearer, and give definitive answers to many problems, especially in the form of negative results.

If in the future, I spend more time on writing about formalism, I would likely discuss one of the above questions, or possibly show some examples of how I think formalism can directly help with moral philosophy.

Cheers