The Gabian History of Mathematics
One of these times where Humanity solved a Big Problem
This is a longish essay (~9K words). If you like computer science, you will likely enjoy reading it and will learn something.
But it is so much more than fun tidbits. This is the story of one of Humanity’s biggest triumphs, and I believe there is a lot to relearn from it.
I hope you will appreciate reading it.
Formalism is the view that maths and logic are primarily about syntax, what one can do within very precise rules of symbol manipulation. This is opposed to maths being about numbers, shapes, or a world of abstract ideas.
Formalism underpins our modern understanding of maths, logic and computer science. It is the core insight that led to the computing revolution and our modern understanding of scientific modelling.
Thanks to our now-formal understanding of logic, we built machines that can automatically check mathematical proofs for us. It’s interesting to reflect on how we got there.
—
Alas, I am not a maths historian.
Fortunately, I am a writer! I have a story of maths that I like to tell, and people like to hear it.
Its key points are all factual.
This is by no means the only story of maths one could tell. For instance, one could focus on social aspects, like the rise of scientific education. That story would connect math progress to the Golden Age of Athens, the Islamic Golden Age and the Age of the Enlightenment.
Nevertheless, my story is about formalism, and I don’t think I have ever seen the story of maths spelled out this way.
—
One of my first essays on this website was on Mathematical Formalism. I was a worse writer back then, but it is short and I recommend reading it, as it will help understanding what I am talking about.
So, without further ado, here is my personal take on the history of maths.
(Some parts get quite technical. Feel free to skip them if you can’t follow, they’re not critical. Or ask questions in the comments about them!)
Summary
I divide the History of Maths into 4 eras:
The Informal Era (–14th). People did maths that was mostly about numbers, and they did so in prose. It was painful.
The Notational Era (14th–19th). Mathematicians discovered and standardised notations. This led to an explosion in maths with many fields being created.
The Foundational Era (late 19th–1930s). Mathematicians, puzzled by the new heights they reached, sought to discover the nature of maths.
The Formalist Era (1930s–). To a large extent, they succeeded! We now consider their solution obvious, and have built most of our techno-scientific stack on top of it.
This is a major adventure, a big win for team Humanity.
We need more wins like this!
The final section lists a few learnings from this win, that we ought to apply to our own problems.
The Informal Era: Prosaic Arithmetic (until ~14th century)
For most of history, maths was pretty informal.
But what do I mean by informal? Isn’t maths the most formal thing?
What I mean is that it was mostly text and people making arguments through text. There was basically no standard mathematical notation aside from numbers.
For instance, the “+” symbol dates from the 14th century, and the “-” one from the 15th! So, when talking about additions, people just did whatever. Some put numbers next to each other, others would say “_ and _” or “the sum of _ and _”. Everyone had their own conventions!
—
Wikipedia has an early algorithm (written by Al-Khwarizmi, whose name led to the word “algorithm”) used to solve a second-degree polynomial.
This algebraic example, from the analogously eponymous book Al-Jabr and Al-Muqabalah (whose title led to the word “Algebra”), is illegible. To me, it reads like hard-to-understand mumbo-jumbo.
It starts with:
If some one says: "You divide ten into two parts: multiply the one by itself; it will be equal to the other taken eighty-one times."
What does this even mean! (And it only gets more confusing as you read more.)
To be clear, this was not another set of conventions, which could be canonically translated to our modern notation. This is just everyone writing down their thoughts in prose, in their own peculiar and internally inconsistent ways.
—
In practice, during the informal times, maths was either accountants counting things, or geniuses writing down their intuitions in prose. Said intuitions were mostly related to arithmetic, which is about counting things in ways more complex than accountants did.
Because all of this was in prose and intuitive, merely understanding someone’s text required a lot of intellectual horsepower.
Some, like Al-Khwarizmi and his algorithms, understood or felt the necessity of having non-ambiguous procedures to do maths.
Of them, a select few went deeper, and aimed to develop non-ambiguous procedures to do logic. Not merely shuffling numbers around, but ensuring that the reasonings and proofs themselves were correct.
I have two go-to examples of this.
—
1) Euclid, who first developed a proper axiomatisation of planar geometry, in his Elements.
This one is close to my heart. When I was young, I was quite fascinated by the type of Straightedge and Compass constructions that one may find in the Elements.
They made for an infinite source of puzzles: given a target drawing, is it possible to define a procedure that lets one do it with only a ruler and a compass?
It was both interesting from a mathematical standpoint, and resulted in beautiful constructions. Even the simplest rosette patterns (“rosaces” in French) like the one below can be quite satisfying.

—
2) Aristotle, who was one of the first to develop a proper rule-based logical system, in Prior Analytics.
It is impressive, as it is one of the earliest attempts to formalise logical reasoning itself.
But aside from its historical context, it holds little value. Like, consider this example, which was later nicknamed in the Middle Ages “Barbara”.
If A is predicated of all B, and B of all C, then A must be predicated of all C.
This just means “If all humans are mammals, and all mammals are animals, then all humans are animals”.
Nevertheless, Aristotelian syllogisms represent a non-trivial fragment of logic, which was considered relevant for a long time.
(If you’re curious, the fragment is the “Monadic Predicate Calculus”, but it doesn’t really matter.)
—
These exceptions are brilliant in how prescient and modern they are. They got so close to our modern formal proof systems!
So close, yet so far. They were missing pretty big components of what was needed to get there. The biggest of them being Notations.
The Notational Era: Maths’ Cambrian Explosion (14th to 19th century)
Simple Symbols (14th to 17th century)
I have already mentioned that “+” and “-” are only like 500 or 600 years old.
Well, they were so convenient that people loved the idea, and started to use more and more symbols.
In an addendum to his Discours de la Méthode from 1637, Descartes writes La Géométrie. In it, he introduces the now-standard notations of x, y and z for variables; as well as a, b, and c for constants.
—
Le Discours de la Méthode is a great book overall. It is quite short, but in it, Descartes introduces, among other things:
The Cartesian Doubt: an approach to epistemology based on extreme scepticism. The OG “source?” guy.
The famous banger “Je pense donc je suis” (“I think, therefore I am”)
A few variants of the ontological argument for the existence of God
And more to our point, he introduces Cartesian Coordinate systems, that let people cleanly bridge the intuitions they had from arithmetic and geometry.
It’s not the best book, for instance, Wikipedia says “Descartes justifies his omissions and obscurities with the remark that much was deliberately omitted "in order to give others the pleasure of discovering [it] for themselves."”
(This is the original “The proof is left as an exercise to the reader.”)
In the same glorious year of 1637, Fermat famously writes that he has a proof of his eponymous theorem, but that it was too big to fit in the margin. (The joke is that the theorem was only proven in 1995 by Wiles, using advanced maths that I can’t understand and that Fermat could never have produced.)
—
Still in the 17th century, Descartes’ contemporaries introduce more and more symbols! Multiplication, division, infinity, pi and more.
Building on top of these new notations, Leibniz and Newton independently both introduce their own notations for what became calculus. One of the biggest shit shows in the history of maths ensued where people fought over who plagiarised whom.
—
In general, the 17th century was a great time for maths. People started using compact notations for what would have taken pages of prose, which let them experiment much faster with their ideas.
Notation was also much more visual, making it easier to spot mistakes. Compare Al-Khwarizmi’s algebraic text to this image:
They express the same concepts.
“Al-Jabr and Al-Muqabalah” specifically referred to “The Balancing Method”, it literally meant “To Complete and Balance”.
Yet, the visual aspect of mathematical notation is just far superior to written prose.
—
These benefits of notations were crucial.
On one hand, notations let mathematicians explore faster. To get to the same place, they had to write much less. Thus they could try more things faster.
On the other hand, notations let mathematicians explore more confidently. It is much easier to check one’s errors in visually arranged equations than in dense prose.
Euler (18th century)
And thus arose the King.
Euler has a long Wikipedia page of topics named after him.
He is also famous for this identity, often described as the most beautiful equation in maths.
In this identity, e, i and π are all notations that he introduced or standardised.
(I always thought “e” stood for “Euler”, but actually, Wikipedia says it is unknown why Euler picked “e” 😊)
Basically, he took all the notations of his time, introduced some of his own, and industrialised the notation process.
By that, I mean the following:
He combed through all the fields of maths that people before him had explored.
He re-analysed each field with a standard set of notations, introducing his own whenever needed.
Using this, he grabbed all the low-hanging fruits. He proved all the results that are “easy” (assuming you’re a genius) to prove when you have access to good notations.
And it turns out that “all the low-hanging fruits” was a lot: he became the most prolific contributor in maths history.
Here are some quotes from Wikipedia to show I am not exaggerating:
Pierre-Simon Laplace said, "Read Euler, read Euler, he is the master of us all"
Carl Friedrich Gauss wrote: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it."
In an effort to avoid naming everything after Euler, some discoveries and theorems are attributed to the first person to have proved them after Euler.
Euler marked a turning point in maths.
Until then, maths was still quite practical in one way or another. For example, Newton was interested in calculus in the context of the laws of motion (where speed is the derivative of position), and Leibniz was interested in calculus in the context of calculating the area under a curve.
Such practicality restricted maths. It held mathematicians back with physical interpretations for most of their concepts, as opposed to embracing the nature of maths as a formal science that only cares for symbol manipulations.
But Euler’s work changed this. It demonstrated how powerful a fully formal approach could be. Unconcerned with the concrete interpretation of its terms, simply applying the same abstract proof techniques to many domains, he single-handedly advanced maths a century forward.
Abstraction (19th century)
The 19th century saw the birth of truly abstract maths.
My favourite example of this is all the fuss around Euclid’s 5th Postulate.
In his Elements (which we mentioned earlier), Euclid introduces 5 postulates. They are meant to capture the intrinsic properties of his geometrical setting, which is the 2D plane.
The first four postulates state:
Between any two points lies a single straight line.
Any line segment can be infinitely extended.
For every point and radius, there is one and only one circle associated with it.
All angles formed by perpendiculars are equal.
All are simple, and obviously correct.
Like, we would not naturally think of them as working assumptions or axioms.
We would think of them as true facts about the world, like, “Of course between two points there’s only a straight line!”
—
The fifth postulate is a bit harder to explain. So I will use an alternative one that is equivalent (assuming the first 4).
This alternative postulate is called Playfair’s Axiom:
Given a line and a point not on it, [there is] one line parallel to the given line can be drawn through the point.
This fifth postulate stunned many mathematicians.
It felt redundant to them. Given Euclid’s definitions and his first four postulates, they felt that one ought to be able to prove it from the first four.
And if you know some maths folklore, you know the punchline: they were wrong.
It is in fact not possible to prove the fifth postulate given the first four! For instance, in hyperbolic geometries, the first four postulates hold, but not the fifth.
Even worse, the first four postulates which we called “obviously correct” earlier? Welp, on a sphere, the first and third postulates do not even hold!
—
This is representative of the tension at the core of mathematical abstraction.
If maths was about numbers or shapes like lines and circles, then in truth, we don’t even need axioms. We are just talking about natural phenomena that we can observe, similar to the laws of physics.
But if we adopt the formalist thesis, that maths is specifically about building axiomatic systems and seeing where they take us; then new horizons unfold.
Until the 19th century, mathematicians were too stuck in a concrete mindset where geometry had to be about Euclidean spaces. Not because they made a conscious choice to study what we now have formalised as Euclidean Spaces. But because this was prima facie obvious, and our first impressions are not that good.
They did not imagine that one could build new abstract objects by artificially removing axioms that felt true and obvious. Let alone imagine that these new abstract objects would be interesting in themselves, and that non-Euclidean spaces would help us accurately describe our universe!
—
Over the course of the 19th century, the mindset of mathematicians changed.
People built non-Euclidean geometries for breakfast.
People built abstract algebraic systems. Where Al-Jabr was the act of balancing equations of numbers, these abstract algebras did not involve numbers. It spawned the flora of monoids, groups, rings, fields, and other delights.
People built abstract polynomials, which transcended polynomials over numbers. This spawned algebraic geometry and more.
This is the beginning of modern maths! Super abstract, and hard to immediately intuitively grasp.
For instance, for concepts that predate modern maths, the motivations were roughly understandable. Newton was interested in differentiation because of position, speed and acceleration being related to each other through it.
But for modern things like Weierstrass’ Elliptic Functions, the “motivation” section doesn’t make sense to normal human beings anymore. It is transcendently abstract. Consider:

The Foundational Era: Questioning Everything (end of 19th and start of 20th century)
The Foundational Crisis (end of 19th century)
Even if formalism was not fully defined and established as a philosophy of maths, it became obvious to maths was transforming.
Maths became less concrete and less hypothetico-deductive. The practice of maths became much less about studying ideal ideas (like numbers or squares) and their properties, as Plato once described.
It was turning more abstract, with mathematicians defining new objects, new systems, and looking at what was happening.
Mathematicians were thus wondering…
If maths was not about real things, what was it about?
This question was the source, itself upstream of many more practical questions.
What even is abstraction? Saying “Maths is the study of abstract things” is not satisfying if we don’t really know what abstraction is.
Why was notation so effective? How come that in less than two centuries, there had been much more progress than in the entire rest of human history?
Why are mathematical proofs so much more solid than other types of proofs? Like, if I am persuaded by a mathematical proof, I will be wrong much less often than when I am persuaded by a philosophical proof. Mathematical proofs are just much more solid.
Despite being so solid, why do mathematical proofs sometimes fail? Sometimes, division by zero can work. But usually, it doesn’t. How do we know when it’s going to fail?
—
Everyone tried to come up with their answers, trying to establish proper foundations for maths.
Some did it in their specific sub-domains.
For instance, Cauchy and Weierstrass were both interested in a proper definition for the infinitesimals used in differentiation. This is what led to the modern ε-δ notion of limits.
Others tried to come up with alternative axiomatic foundations for geometry, to answer the shortcomings of Euclid’s.
Still others went for the true definition of numbers. This led to the Peano axioms for the natural numbers (a definition of numbers based on properties of addition and multiplication) and Dedekind cuts for real numbers.
—
But from my point of view, the most interesting endeavour was to try to understand what all of maths was about. What were proofs? What were mathematical entities?
This is the true foundational crisis.
And when people tried to come up with a universal answer like set theory, paradoxes abounded.
Instead, people started moving towards more pragmatic questions. Like, “How could a mathematician, using an effective procedure, precisely solve this pragmatic problem?”
In these questions, the notion of an “effective procedure” was often mentioned. This is the direct parent of our modern-day algorithms.
Hilbert’s Problems (1900)
To deal with this foundational crisis, Hilbert used a great intellectual trick, too often underrated.
He wrote a list.
He took what he thought were the most revealing problems of his time, phrased them in the most useful way he could think of, and listed them.
Where before, the foundational crisis was a bit too philosophical, it became much clearer.
Hilbert simply wrote down all the important problems of his time.
I believe that in his list, these three problems were especially important.
The Second Problem
Proving that the axioms of arithmetic are consistent (ie: that they do not imply a contradiction).
This is a great intuition: if one can prove that the axioms of their system are consistent, then they have established that there is no paradox and that the system in question is solid.
This was partly motivated by all the paradoxes and inconsistencies that came from early versions of set theory.
The Tenth Problem
Building an effective decision procedure to check whether a given polynomial Diophantine equation with integer coefficients has an integer solution.
This is yet another great intuition: the goal is to build a mechanical decision procedure. On Wikipedia, it is described as him asking for an algorithm; but this is anachronistic. This problem helped consolidate the intuition that would later become the algorithm.
The Twenty-Fourth Problem
Developing a general theory of the method of proof in maths.
In my opinion, this problem is the most important one, and unfortunately went unpublished!
This is him calling in advance what will become the study of formal proof systems, and his future programme.
This problem goes very deep.
For instance, Hilbert considered that an answer to this problem should let us formalise the notion of which proof of a theorem is the simplest.
This “simplest proof” concept was much more refined than even our modern study of proof length complexity.
Hilbert’s Programme (1920s)
Thanks to Hilbert’s list, a lot of progress was made toward formalising proofs, logic, consistency and other similar concepts.
The culmination of these efforts was Hilbert’s Programme.
The idea of the programme was to ground all of maths in a minimal axiomatic formal proof system.
The system ought to be definitively proven coherent (formally free of contradictions) to avoid the past misfortunes and paradoxes.
Once this was done, the final goal of the programme would be to define an effective procedure that could take any statement expressed in this formal system, and prove whether it is true or false, still within the formal system.
This challenge was called the Entscheidungsproblem.
Hilbert’s challenge was extremely ambitious! His whole programme was about creating an operating system to then define a procedure that could solve all of maths.
But it might have been too ambitious.
Gödel’s first Incompleteness Theorem (1931)
The first blow to Hilbert’s programme was Gödel’s first incompleteness theorem.
This result has been pseudo-intellectualised so much. It’s comparable in scope to how people use quantum mechanics to “prove” things about consciousness and drugs.
For instance, people try to use it to show that humans can necessarily do more than machines and there will be human ethical truths that machines can not come up with. The incompleteness theorems’ misuses are so pervasive that an actual book has been dedicated in large part to them.
But no, Gödel’s result is relatively simple. And it is purely formal.
Let’s take a less confusing example first.
Gödel’s Law
Most governments can pass pretty advanced laws. Like, it is possible to pass:
A normal law that says “Blue helmets are forbidden”
A meta law that says “It is forbidden to pass a law forbidding blue helmets”
A self-referential law that has a clause that says “This law will expire in 2 years”
Well. If a legislator were so inclined, they could submit the Gödel Law: “This law can never be passed into law.”
If the code of law is sound, then the Gödel Law can never pass, as it would contradict itself.
But then, if you think about it… It means the Gödel Law is already in action! The Gödel Law precisely specifies that it can never pass.
Thus, the code of law is not complete: even though the content of Gödel Law is true, or de facto in effect; it may never be so de jure.
This is a fun quirk. And except if we wanted the code of law to be able to logically codify everything, we shouldn’t be too sad about it.
Specifically, we should not infer from the Gödel Law anything about what the code of law can regulate in practice. This has no bearing on practical matters.
This doesn’t tell us how hard it is to regulate markets, presidential terms or anything that is not deeply self-referential.
The Gödel law doesn’t tell us anything about policy, political philosophy, or governance. It is purely a formal artefact that makes constitutional lawyers laugh.
Gödel’s Proof
Well, now, let’s move on to formal proof systems. Gödel has basically shown two things.
If a proof system is powerful enough, it can represent itself.
Gödel has shown that in an Advanced enough Proof System (let’s call it APS), one can write:
Concrete statements like “2 + 2 = 4”
Meta statements like “APS admits a proof that 2 + 2 = 4”
Self-referential statements like “APS admits a proof of this self-referential statement”
Specifically, he has shown that the proof system doesn’t need to be that advanced. It just need to have an encoding of basic arithmetic: natural numbers, addition and multiplication. His method is called Gödel numbering, and it’s quite convoluted.
—
A sound proof system that can represent itself has statements it cannot prove.
He has also shown that in particular, he could write a Gödel Statement that says “This very statement is not provable in APS”.
If the proof system is logically sound (it can only prove true things), then the Gödel Statement cannot be proven. Proving it would be an example of proving a false thing.
Thus, it is true that the Gödel Statement is at the very least not provable.
But then, it means that the Gödel Statement is true, as what it says is that it cannot be proven!
So it means that there is a statement that is both true and unprovable in APS.
This is what we mean by “incompleteness”.
That’s it.
It’s not about there being “intrinsically unknowable things” or any of the bullshit interpretations that I have read.
This doesn’t tell us anything about the human spirit not being study-able by science or maths not being able to talk about art.
It’s just a formal thing that is irrelevant to most people and even most mathematicians.
—
But this is enough to defeat Hilbert’s Programme!
One should remember that Hilbert’s Programme was extremely ambitious. It was a universal hope, and any single counterexample thus suffices to shatter it.
Follow-ups (1930s)
After Gödel’s first incompleteness theorem, a few other theorems followed, following the same template, dealing subsequent blows to Hilbert’s programme.
Tarski’s Undefinability Theorem
Tarski’s undefinability theorem (from 1933) says that in a proof system powerful enough, one cannot define a predicate for truth.
The proof is even simpler conceptually than Gödel’s!
Let’s assume that in my proof system, I can say “_ is true” for any sentence.
Let’s further assume that my proof system is powerful enough for self-referentiality, and that it has negation built-in.
Then I can write the Tarski Sentence “This sentence itself is not true”, which is a direct instance of the liar paradox.
This is not about whether we can prove the Tarski Sentence or not. This is about whether it is actually possible to even formally define it in a proof system self-referential enough. And the answer is no.
So, for the very same reason that it is not possible to define an oracle that is always truthful if it is allowed to say “I am lying”, a strong enough formal proof system cannot define a predicate that is always truthful.
This is exactly as profound as the liar paradox.

Gödel’s Second Incompleteness Theorem
Let’s keep going!
Gödel’s second incompleteness theorem is even more self-referential.
Feel free to just jump to the bolded sentences below if you don’t want to hurt your mind with more self-reference.
Assume an Advanced Proof System (APS) is strong enough to be self-referential, then we can express…
Concrete statements like “2 + 2 = 4”
Meta statements like “2 + 2 is provable in APS”
Self-referential statements like the Gödel Statement “I am not provable in APS”
In APS, we have seen that the Gödel Statement was not provable, and yet it was true.
However, it is provable that “If the Gödel Statement is provable in APS, then there is a proof of contradiction in APS”.
By contraposition, we get a proof that “If there is no proof of contradiction in APS, then the Gödel Statement is not provable in APS”, which is just “If there is no proof of contradiction in APS, then the Gödel Statement is true”.
Thus, we prove that there’s no contradiction in APS, else, this would let us prove the Gödel Statement correct, which we know is not provable from his first incompleteness theorem.
This is a much more direct hit to Hilbert’s Program: it means a non-trivial proof system cannot prove that it is free of contradictions.
Turing’s proof
The final nail in the coffin to Hilbert’s Programme was from Alonzo Church and Alan Turing, both independently proving its final goal was impossible in 1936.
I’ll stick to a simplification of Turing’s proof, because it’s the most accessible one, and arguably the most impactful one too.
The proof comes from his paper “On Computable Numbers, with an Application to the Entscheidungsproblem”.
It features several key components…
—
Turing starts by defining “automatic machines”, which are now called Turing Machines.
This is arguably the birth of computer science.
Turing defines a minimal formal model of computation, for the purpose of proving Hilbert wrong.
Nowadays, his model of computation is still studied as such, so much so that an algorithm could nowadays be defined as “whatever can be implemented in a Turing Machine”.
—
Turing then defines the Halting Problem, the problem of writing a Turing Machine that predicts whether another Turing Machine runs forever or eventually halts.
Turing shows that solving the Halting problem is impossible, using a proof technique very similar to Tarski and Gödel: a diagonal argument.
For simplicity purposes, I’ll explain the proof using the modern Python programming language instead of Turing machines.
Let’s assume that there was a Python program that let us know whether a program halted or looped forever. Let’s call it “oracle”.
Then we could just write a “liar” program that is meant to defeat the oracle. It just looks at what the oracle predict it would do, and then does the opposite. In Python, this is:
If the liar sees that the oracle predicts that it would halt, then it decides to run forever.
Else, if it sees that the oracle predicts that it runs forever, then it halts immediately.
Thus, in Python, as well as with Turing Machines, it is not possible to have a program that solves the Halting Problem.
—
Finally, Turing proves that if we could write a program to solve the Entscheidungsproblem, then we could use it to write another one to solve the Halting Problem.
This is proof by reduction, which is about transforming a problem into another one.
And this reduction does something very deep. It shows that the process of finding a proof is general and powerful enough to encode any arbitrary computation.
In logical terms, he shows that we can write the following logical formula, showing that there is some time value for which a Machine halts on some given Input.
Thus, an algorithm to find a proof for an arbitrary statement would let us solve the Halting Problem, which we know to be impossible.
Thus, there is no such algorithm.
This is huge.
This basically turns Hilbert’s Programme on its head!
Hilbert’s Programme was about defining an algorithm to prove everything.
Instead, Turing had shown that it was impossible, precisely because one could use proofs to implement any algorithm!
The result of the Programme
The 1930s were the culmination of more than 50 years of work on the foundations of maths.
Through Hilbert’s list of Problems, his Programme and his Entscheidungsproblem challenge, mathematicians got a precise roadmap to develop a deep understanding of formalism.
Before then, people were lost on how to deal with the nature of maths. It seemed overly philosophical or metaphysical.
But Hilbert’s formalist agenda attempted to mathematically ground it. To definitively answer a metaphysical question through maths.
Then the work of Gödel paved the way for the formal treatment of self-reference.
Then the work of Tarski established a clear separation between formal syntax and intuitive meanings (semantics). The culmination of which would later be Model Theory, the field of formally treating semantics.
Then the joint work of Turing and Church created our modern understanding of computability which is captured in the Church-Turing Thesis, the idea that all formalisms for “effective procedures” are roughly equivalent.
All of these were about the strict application of simple formal rules.
We set out to fully resolve a question which appeared to be philosophical, as vague as the nature of maths. We put our brightest minds to it.
In the spans of a few decades, we created a full theory of mathematical proofs, of formal truth, and of computation.
This may have not met the high expectations of Hilbert, but it’s still got about everything else going for it.
The foundational crisis got resolved. Instead of a single sharp answer, its resolution was more one of progressively building over decades an understanding of formal maths and of its limitations.
The Formalist Era (1940 onwards)
The Answers
So, what was the answer of formalism to all the questions we had?
On the nature of maths
Maths is not a science where one makes hypotheses and tests them. It’s unlike a natural science or a social science.
It is a formal science! This means it is fully abstract.
I explain more about it in my essay on formalism, but quickly: it means that it is about symbolic manipulation, regardless of any meaning we could ascribe to these symbols.
On the effectiveness of notation
Before notations, mathematicians were only relying on their intuitions and platonist preconception of various concepts.
This intrinsically limited them to the strength of their imagination and of their intellect.
With notations, it became much easier for mathematicians to transcend their naive intuitions, by only focusing on the formal rules of maths regardless of what things truly meant.
Instead, with this new way of doing maths, the proofs became the ground truth, and intuition were only a source of inspiration.
This empirically let them go much further than their intuitions, pushing calculus past its physical grounding, pushing geometry past its euclidean interpretation, and so on.
Euler was the biggest example of this.
In essence, by letting people mindlessly apply derivation rules through compact notations, it separated the activity of coming up with interesting formal rules from the activity of coming up with situations where these formal rules directly apply.
—
For instance, when one manipulates the axioms of Peano Arithmetic that defined the numbers in terms of the properties of addition and multiplication, they are not merely dealing with the standard understanding of natural numbers.
There are structures, where the axioms of Peano Arithmetic are valid, that are nevertheless “bigger” than just the natural numbers. These structures are called non-standard models.
Non-standard models are the key to another insight about Gödel’s incompleteness theorem, which is that the truth of the Gödel statement is actually relative to the type of numbers we have in mind when we think of Peano Arithmetic.
Past understandings of maths would have completely ignored such non-standard models, and would not have even realised that the axioms of Peano Arithmetic could not fully capture what we meant by natural numbers.
It is only by following notations without encumbering ourselves with preconceived interpretations that we managed to get there. And the more we went through the motions of notations, the more we got out of them.
On why mathematical proofs are so much more solid than other types of proofs
This comes from the fact that we can actually list all of the axioms and all of the deduction rules that we use in formal proof systems.
This lets anyone replicate any proof, so much so that we can have computers do it. And it is what makes formal proof much more reliable: it is very easy to find mistakes in them.
Furthermore, by virtue of listing all the axioms, we can standardise which axioms we use and collectively benefit from their study.
For instance, we talked a lot about the consistency and completeness of Peano Arithmetic, but a lot of similar work was later done on ZF/ZFC, a foundational set theory more practical than Peano Arithmetic for “everyday” maths.
People did a lot of work around the consistency of ZF and other related axiomatic theories. People stress tested these axioms, checked in which circumstances they were necessary, etc.
This standardisation makes maths especially resilient, even compared to other formal fields, where the axioms used in practice are not necessarily standardised across its practitioners.
On why mathematical proofs nevertheless sometimes fail
The formalist account of maths gives a complete answer to this question!
Namely, either…
The formal proof system in which the proof is expressed is inconsistent.
The specific formal proof does not follow the rules of the formal proof system.
The proof is correct, but is applied to a situation that does not precisely match its axiomatic requirements.
For example…
Defining new formalisms creates a risk of (1). If they are not well thought through and battle tested, they risk being proven inconsistent.
Doing maths “intuitively” creates a massive risk of (2), where it feels like we have the full proof in our mind, but we actually start feeling stupid when we try to formalise it with a proof assistant like Coq.
Any philosophical mishandling of maths is (3). It may be any of the countless misapplications of utilitarianism and game theory, or the eternal spiritual torture of both Gödel’s incompleteness theorems and quantum equations.
Thanks to formalism, we now have a mechanistic understanding of what an invalid proof is! It went from something extremely metaphysical (“Sometimes, we may have arguments that sound correct to people and yet end up wrong”) to an object we can encode in a fully automated machine.
The Applications
Ok, I talked a lot about what formalism meant and sang praises to it.
But the proverbial proof is in the pudding.
So how cool has everything gotten since we started using our formalist understanding everywhere?
The Modern Computer
There were computers before 1930. But almost all of them were special-purpose arithmetic engines.
For instance, the Arithmometer was a desktop computer that let one add/multiply/subtract/divide two numbers. The Arithmometer held a de facto monopoly for 30 years in the entire world, which is hard to imagine nowadays.
Similarly, IBM got started with the Tabulating Machine, which was basically a machine special-purpose built to read and help aggregate information stored on punch cards (the mechanical ancestor of memory cards). This is the oldest system that I would count as an Excel. The fun story here is that a particularly bad US census (which took 8 years to complete) motivated the creation of the machine.
—
There were some who thought beyond special-purpose machines.
The idea of an engine that could process many more types of operations had already been in the air for a century, thanks to Babbage’s Analytical Engine from 1837. This was a prescient design of a machine that supported all the basic algebraic expressions, as well as some conditional and loops.
From Babbage’s design, Ada Lovelace suggested a program that would have let one calculate Bernoulli’s numbers using the Analytical Engine.
But the Analytical Engine was much too complicated: it was meant to work in decimals as opposed to binary, with a 1000 numbers, and built-in functions for all of arithmetic. Thus it was never built. The vague idea of “generality” was not enough by itself.
—
Much later though, as part of his proof rejecting the Entscheidungsproblem, Turing had to define a new type of computer, one that would be self-referential enough to define its own working rules as a program, represented in memory. The new type of computer was later called Turing Machine. And the special program encoding its own rules was the Universal Turing Machine.
It seems obvious nowadays, but back then, programs were separate from memory. The insight of code as data is modern! Without it, it would have been extremely hard to build operating systems, programming languages, or static analysers. And it would have been straight-up impossible to have self-modifying code or dynamic optimisers.
But this insight is precisely what was needed to reject the Entscheidungsproblem! Turing’s proof started by defining a programming model that was powerful enough to be general and self-referential, yet small enough (as opposed to Babbage’s designs) such that it could easily be reduced to first-order logic with Peano Arithmetic.
This new computing model, the Turing Machine (and soon after the equivalent but more practical Von Neumann Architecture) was directly responsible for computing as we now understand it.
Computational Complexity Theory
The 1930s were mostly focused on Computability, which was the question of whether there existed “effective procedures” for various problems.
Here, “effective” is a bit of a misnomer. Back then, “effective procedure” just meant “mechanical and deterministic”.
But now, we live in a world that has formalised computation and has done so for decades. When we think about the efficiency of a procedure, we think about more than “Is it theoretically possible to define a program that performs a specific task”.
We think primarily about its speed, and its memory consumption.
The field dedicated to studying this (among other things) is Computational Complexity Theory, and is directly downstream of the formalist tradition.
Its basic techniques are actually the same as the ones used in computability! Self-referential contradictions, as well as formally reducing problems to others.
Beyond formalising the considerations around the efficiency of procedures, Computational Complexity Theory lets us formalise a large array of real-time trade-offs.
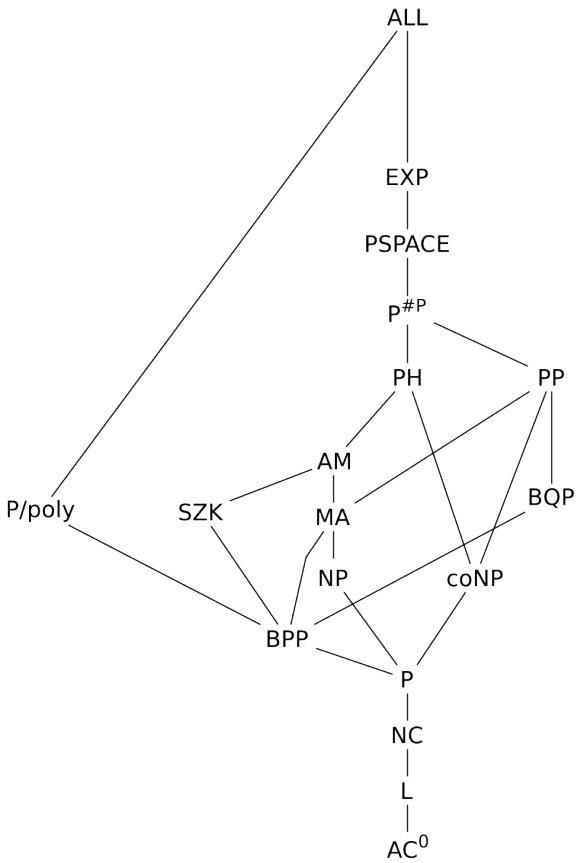
Computational Complexity Theory has many philosophical implications which leads to a more refined vision of the world. Scott Aaronson wrote an insightful paper about this.
All formal sciences
Formalism has expanded far beyond metamathematics and theoretical computer science.
Many fields now have their formal variants, like economics and game theory, or biology and computational biology.
Most fields use formal techniques, whether it is model-based computer simulations or just copious amounts of data science.
New fields have also been created that are exclusively formal, like programming, automated theorem proving or cryptography.
We now are fish in the water. We live in the formal era. Formalism is everywhere, and it feels like normal.
It is hard to imagine a pre-formal world, where people did not immediately understand why it is possible to write a program interpreter, when there are so many online tutorials anyone can use to create their very own programming language, let alone merely interpreting an existing one like LISP.
It is hard to imagine a pre-formal world, when people were confused about what made a proof rigorous, and when geniuses made mistakes that a smart high-schooler would immediately notice.
The Spirit of the Formalist Arc (into the future!)
Doing Things Well
For me, this arc of human history is about something deep.
It is the result of times when geniuses tried to do things thoroughly.
When these maths geniuses noticed that notations and maths worked really well, they didn’t go “I guess it’s just that maths is good lol”.
They took what felt like a non-scientific question, the nature of maths, and turned it into a scientific question.
They tried to understand what really made maths work, reverse engineer it, and completely solve it.
And they did! In a few decades, they unlocked an entire new section of the technological tree. They created a large part of the modern world! Automation and information technologies are directly downstream of their effort.
—
Nowadays, our geniuses seem very meek, content to just explore their very specific niches and to profit from systems which they do not understand. I believe they should instead try to unravel the crucial mysteries of our times.
In the past, many Greeks thought that the stars were divine beings or heroes immortalised in the heavens, that natural disasters were caused by the gods, or that Chaos birthed Gaia. And we transcended these beliefs!
There are crucial topics where we are as lost as mathematicians were in the past, and where we should try to pull what we pulled with formalism: a definitive answer to these deep questions.
Right now, these crucial topics might seem non-scientific, but the history of science (including formal sciences!) has been a long conquest of what was thought to be the realm of metaphysics and supernatural entities.
Governance
The Enlightenment was great. Many great thinkers sought to come up with a alternative to kingdom that was better for the people, and they largely did.
This led to a governance explosion in the 18th and 19th centuries.
Sadly, since then, we have mostly stalled. Our governments are still using the Separation of Powers in three branches (legislative, executive and judiciary) that Montesquieu spontaneously conceived in 1748.
On the theoretical side, we have done a lot! We have developed game theory, public choice theory, voting theory and even distributed consensus algorithms.
And yet. Very little improvement in governance.
—
The biggest example of this stagnancy is voting.
Voting every couple of years was the best that our ancestors could do with the technologies of their time.
A time when the fastest ways to transmit information were homing pigeons and horse carriages! When countries had much less transportation infrastructure like railways or airports. When people were much less educated and knowledgeable than they are now.
We now have the Internet, which lets us transmit information as fast as physics will let us and most people graduate from high school.
But we still use anachronistic voting systems. This is ridiculous!
—
There are so many problems in governance.
How can we integrate experts into policy making, with proper checks and balances to avoid academic capture and the politicisation of science?
How can we hold politicians accountable for their lies, and ensure they take action when it matters?
How can we reliably deal with negative-sum games?
How can we deal with entrenched interests, special interests and concentrated interests?
It seems quite sad to me that we are not any closer to a solution on any of them than we were 20 years ago.
But let’s move to another topic close to my heart, where we also need a reckoning, similar to maths’ foundational crisis.
Morals
Our morals have changed a lot in the recent decades, and a fair share of it can be qualified as moral progress.
Sadly though, the vocabulary of morals has not changed much. We can find most of it in the Universal Declaration of Human Rights from 1949.
To be clear, there have been a couple of moral innovations, like Data Rights, Privacy Rights, Indigenous Rights as well as Sustainability for the Future.
But at large, it doesn’t feel like we made that much progress on identifying Human Values and good ways to trade them off. We are still thinking in the same terms, through the same types of principles, many that can be traced to 18th century and have been reused as is.

—
I don’t expect that debating morals with my contemporaries would make me so much smarter than debating with people from the 1950s.
It looks like we are still as confused as we were before.
This is in sharp contrast with technical topics.
I expect that discussions on any technical topic will be much richer in 2025 than in the 1950s, and that any scientist from back then would love the opportunity to have access to our current body of knowledge.
It is a shame that this is not the case for morals.
More!
There are so many more important topics where we are thoroughly confused.
Psychology and Sociology. How do people work? How should we reason about people? How should we predict our own behaviour?
Meditation and Introspection. It looks like we can get many benefits from thinking about the correct stuff. Like making better decisions, having more control over our attention and curiosity, being calmer and less stressed, learning faster, and feeling better. Yet there is no scientific body of meditation/introspection techniques that I can use. It’s usually a bunch of spiritual new-age mumbo-jumbo. Aaaah!
Management. What are the best ways to work together? In non-profits, for-profits, in families and in friend groups, I have always seen people use a combination of natural talent, experience and heuristics. We ought to build a science of management that actually lets us build better organisations!
What can we learn?
I believe there are a few lessons we can derive from the Formalist Arc.
1. Lots of work
The first one is that solving formalism required a lot of concentrated work from a lot of geniuses.
Instead of working in finance, SaaS, GenAI or ad-tech, they were working on this.
Instead of maximising their impact factor or publishing one more paper they did not believe in, they were working on this.
This took sustained work over decades from the brightest of their time.
Where are today’s brightest spending their time?
—
Personally, I find it quite sad that the brightest people I know are not trying to thoroughly and scientifically solve the problems I mentioned.
I find it sad that many play too much video games or waste their talent on questions that are too narrow and irrelevant.
It takes a lot of work from very driven geniuses to solve such problems, and we are not harnessing the ones we have.
We should be planning for many such projects. We are not lacking in important problems that we must solve.
I think there is just a big mismatch, and that the mismatch is mostly explained in this article. (Tl;dr: what people spend their time on is rarely the result of a deliberate process, and this is especially true for geniuses.)
2. Lots of ambition
The second one is that ambition is crucial.
Many of them sought to fully solve maths. The most emblematic of which was Hilbert’s Programme.
This was not vain ambition. Hilbert’s Programme was specifically about designing methods that could in principle solve maths.
This was not intellectual masturbation either. Hilbert’s Programme was so meaningful that rejecting it was enough to usher in the formalist era.
It was a serious ambition, with a solid plan to solve The Big Problem. The plan was good, and it needed to be good such that failure would also be informative.
—
In contrast, I don’t know of an equivalent of Hilbert’s Programme in any of the fields I have outlined earlier.
I simply believe that despite all of the hype around getting rich, startups and VCs, we are just much less ambitious.
“I will make a gazillion money by building the next Netflix or Uber” seems so much less ambitious than “I will meaningfully contribute to an understanding maths so thorough that it will affect Humanity’s entire tech tree”.
“I will cut a lot of government spending” seems so much less ambitious than “I will solve governance and the solutions will be so good that both politicians and governments will be forced to pick them to stay competitive”.
It might be that we can’t replicate the methods that let us solve maths in governance or morals. But I don’t care much for this thought. Until we try the Obvious Thing and fail, I don’t think we ought to give much attention to pessimists and those who say we can’t do things.
—
To be fair, I believe many people are simply afraid of being too ambitious. And the fear makes sense to some extent.
Some people are so obsessed with power that they are willing to hurt others over it. They will trample over everyone else, and do things that they would consider immoral if anyone else was to do the same.
Even worse, most people who are too ambitious are just untethered to reality. They become megalomaniac, narcissistic or even the “I will be the Second Coming of Christ” type of people.
However, I think that it is possible to cultivate a good type of ambition.
The type of ambition where we contribute toward a critical intellectual project in a grounded manner.
The type of ambition where we want to help and strengthen as many people as possible.
This story is a nice way to internalise what this good type of ambition looks like.
3. Long Lists
The third lesson is that lists are good.
Too many people who want to work on a crucial problem try to assume its complexity away.
—
I had a recent discussion about governance. My interlocutor then told me about their economist friend who had an ideal model of [something] and I sadly sighed.
I do not care much for ideal models. Not because they can’t be useful (I’m a formalist, of course I think ideal models can be useful!).
Just because people who work on ideal models tend to be the type of people who will do anything but engage with the real world. They will never be people who tried to implement better governance principles in an organisation, failed, and are now tackling the bottlenecks to doing it.
They will be people who find talking about these specific ideal models interesting.
What they will never do is write a long list of desiderata and constraints that they got from the real world, which their models should satisfy.
—
Hilbert’s Problems were a great example of this.
Even maths, the purest field ever, was big and messy. And Hilbert embraced the mess. 23 problems, all from different subfields and of different natures, meant to surround maths from every angle.
With his understanding of the time, he put down in writing what he thought were the most relevant problems of maths, with various precision levels.
(To be fair, I’d say he was still too shy! His 24th problem, which he did not publish, was the best one.)
—
I want Hilbert’s Problems of Morals, of Governance, and of everything!
How can a field be considered a serious field if I cannot even see its top 20 open problems? If I cannot see them, that’s because scientists are not constantly tracking them.
This in turn reveals that they are not collectively looking at a clear North Star. In other words, there is no big picture. They are much too lost in short-term fads and turbulences.
If I am to consider a field seriously, at the very least, it should have a list.
Conclusion
I love the story of formalism for many reasons.
Some are objective: I truly believe it is one of the core insights behind modern science.
Some are more personal: I investigated formalism by myself quite a lot, before learning about it from others.
But the biggest reason is that it is inspiring.
Through sheer collective intellectual genius, we solved one of the most metaphysical questions (“Why does maths work?”).
We worked at operationalising it for decades until we could solve it.
And then we did solve it. The response we found was unexpected, and so important that much (most?) of our modern world relies on it.
I think we should do more of that.
—
I did not mean for this article to be that long. Sorry!
But this is a story that I love telling orally, and I must get better at writing down my stories.
So here it is!
On this, cheers, and have a nice day!



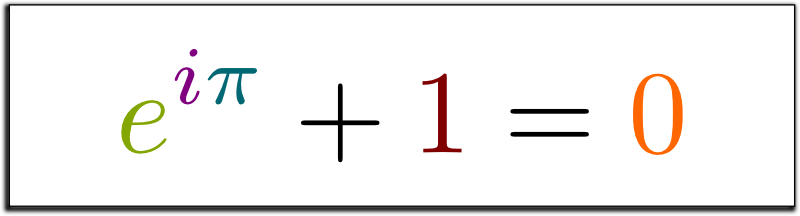



I woke up 3AM this morning, probably because my girlfriend has led us to experiment with Italian-style blankets over a duvet (it sucks, we're moving back).
Gabe, in a way you ruined my night, I got my phone and started reading, and then I couldn't stop and didn't sleep anymore.
I thoroughly enjoyed your piece.
To me it's of great coincidence that you know so much about this topic, because I subscribed to your mailing list for AI safety, and independently have been obsessed with metamathematics this summer, prompted by having just finished Russel's History of Western Philosophy and seeing how formalism solved a large part of philosophy, and criticizing Penrose for thinking Gödel's incompleteness says anything about consciousness, and finally reading GEB (which as been staring down at me all my life from my (now late) dad's bookshelf) (and enjoying what a dated perspective it seems to be unfolding on AI).
I couldn't agree more on what a magnificent achievement it has been of humanity. It's so beautiful
Will be musing more about it in the coming days,
David
> If some one says: "You divide ten into two parts: multiply the one by itself; it will be equal to the other taken eighty-one times."
10 = 9 + 1
9^2 = 1 * 81